Startseite
Jahrgang wählen  .... ....  .... ....  |
|
 * * * * * * * * * * W W @ @ * * * * ▼▼ ▼▼  |
|
Fortsetzung siehe folgende Jahrgänge oben |
|
 * * |
|
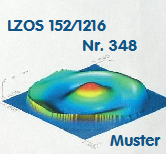 |
A062C * LZOS for APM 152/1216 Nr. 384Der folgende Bericht ist eher als Beispiel gedacht, zu welchen Ergebnissen bestimmte Tests führen, wenn die opt. Qualität |
 |
A109A * William FLT 132 F7 - Vorsicht beim ZerlegenDie Linsenfassung dieses Triplet APO's scheint augenblicklich unter verschiedenen Labels weit verbreitet zu sein. Das System links |
 |
E081 * Der das Gras wachsen hört . . . Beschichtung/DickeDie "GscheidHaferl" <bayerischer Ausdruck> wachsen auch bei den Hobby-Astronomen immer wieder nach. So konfrontierte unlängst |
 |
A062B-LZOS_for_APM175-1400 Portugal - auf Herz und Nieren geprüftBei derartigen Objektiven frage ich lieber nicht nach dem Preis - nicht jeder wird in seiner Schatulle den nötigen Betrag zusammen-kratzen können. |
 |
F041B Artificial Sky Test Unit für MassimoDie Herstellung einer Artificial Sky Test Unit ist eher die Arbeit eines Uhrmachers. Das entscheidende Bauteil ist ein kleiner 4x5 mm^2 Planspiegel, |
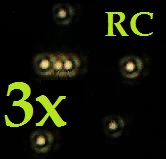 |
094A * GSO 8-RC Zentrierung in drei SchrittenEs ist in erster Linie ein fotografisches System. Das bedeutet, daß schon wegen der großen Obstruktion eine visuelle Benutzung nicht |
|
|
 |
F054B Überlegungen zu Microrauhheit und deren Messung Bei dieser Thematik geht es um die Flächen-Rauhheit/Glätte bei Spiegel-Systemen, also in einem Bereich von spiegelnden |
 |
C083 SkyVision - Spiegel und Teleskope, Hersteller in FrankreichIm Nachbar-Land Frankreich, hat sich offenbar die Erkenntnis durchgesetzt, daß glatte Spiegel für die Beobachtung empfehlenswerter sind. |
 |
C082 Teleskop Austria Tommy Nawratil 10"GSO Quarz Dieser GSO Quarz-Newton-Spiegel wurde zweimal geprüft. Und weil die Ergebnisse nahezu deckungsgleich ausfielen, kontaktiere ich mit |
|
|
 |
D021-02 Kriterien beim Kauf von SC-Systemen die von Celestron und Meade produzierten Schmidt-Cassegrain-Systeme, sind die Kombination eines Cassegrain-Systems mit sphä- |
|
|
 |
H200 BTM 2014 Pneumatische Nachführung - die Idee mit Pfiff Das Bayerische Teleskop Meeting organisiert von Uli Zehndbauer am alten Standort am Osterberg, Pfünz, hatte auch 2014 |
|
|
 |
C061A Bei einem Newton-System müssen Haupt- und ellipt. Plan-Spiegel bestimmten Qualitäts-Normen entsprechen. Dabei kann |
|
|
 |
B011A * SkyWatcher 100/900 ED-APO ohne/mit Glasweg Das Teleskop hat zwar einen neuen Tubus verpaßt bekommen, aber das Objektiv selbst dürfte immer noch der "alte" ED- |
|
|
 |
D048A * Reparatur eines C11 280-2800 Nr 956936 Bei optischen Systemen stellt sich bei einem Test auf der opt. Bank jedesmal die Frage, wieviel von den Fehlern Astigma- |
|
|
 |
A037A * Zeiss APQ # 96998 100/640 mit Glasweg verwenden Bei diesem Zeiss APQ sollte man niemals einen Zenit-Spiegel verwenden wollen. In einem solchen Falle würde die Farbrein- |
 |
B045_01* APM Fernglas 100mm ED-Apo DoppelBilder-Zentrierung Neben dem KOWA Highlander Prominar 82/450 das bei 50-facher Vergrößerung brilliante Bilder abliefert, gibt es bei APM eben- |
 |
A103A Das Internet verspricht viel. Im vorliegenden Fall wird der versprochene Mindest-Strehl von 0.96 sogar weit übertroffen - Strehl 0.99, wenn, ja wenn nicht zwei massive Fehler die "Schönheit" der Optik deutlich reduzieren würde. Auch ein verkippter Fokuser könnte die Ursache der Mängel sein - dann wären das die Ergebnisse einer Feldmessung also nicht auf der opt. Achse. |
 |
C054A 20" Newton-Spiegel f/4.5Dieser 20-Zöller f/4.5 sei ein Produkt von Oldham, UK, sagt der Sternfreund. Immerhin ist die Spiegelfläche sehr glatt ausgefallen |
 |
H999 * 2014 ICS - AstrofestDiesmal nannten sie es Astro-Fest - Familien-Fest hätte auch gut gepaßt. Wenn sich die Sternfreunde aus dem |
 |
C024A Astigmatismus - die Erde ist eine ScheibeManche Überzeugungen sind monolithisch und haben eine lange Überlebensdauer. Es war zwar schon lange bekannt, |
 |
D021-01 * OMC 140 Orion UK F/14Bei einem einem Öffnungsverhältnis von 140/2000 bzw. F/14.28 sollte man von einem visuell intendierten Teleskop ausgehen. |
 |
A065A APM Triplet APO 80/480 + Ric Reducer, 50 mm BildfelddurchmesserThis telescope is a super aprochromatic lens with a RC_index number of 0.1984. In combination with the Riccardi Reducer |
 |
D049A Takahashi TSC - Schmidt-Cassegrain 225-2700 F12Der Strehl-Wert ist für die Beurteilung zu einseitig. Die Standard-Tests liefern weitere Informationen:
- die sphärische Abweichung liegt unter PV L/15 |
 |
D052A 16inch SchmidtCassegrain - ein deutsches ProduktDer vorliegende Fall ist deswegen bemerkenswert, weil ein Spiegelschleifer in der Szene sich vor Jahren ein 16-inch Schmidt-Cassegrain-System |
 |
A052A - 90% Nachdenken und 10% FeinmotorikDieser TMB-APO war bereits im Sept. 2008 bei mir, und hatte mich zu diesem Bericht verleitet: A052 * TMB APO Nr. 092 (152/1216) |
 |
Kombination TS Photoline 102/714 mm F/7 + TS Flat 2.5 bis 4.0° BildwinkelIn den letzten Jahren wird zu den eigentlich kleinen und schnellen Apochromaten auch noch Flattner angeboten. So wird bei vielen Kombination |
 |
A120 SkyWatcher Esprit 150 ED APO perfekt für H-alphaUm eine Teleskop-Optik richtig beurteilen zu können, sollte man unbedingt wissen, wofür sie gebaut worden ist bzw. mit welchen Erwartungen sie gekauft und später verwendet werden soll. Den "Allrounder" gibt es auch auf dem Teleskop-Sektor kaum, auch weil uns heute ein Qualitäts-Bewußtsein fehlt, daß man für ordentliche Qualität auch einen angemessenen Preis zu zahlen hätte. Je nach Verwendung läßt sich daher ein Fernrohr ganz verschieden beurteilen ... |
 |
A126 Astreya Super APO neu zentriertAn diesem Objektiv hatte der Sternfreund keine große Freude mehr. Beim Kauf aus zweiter Hand hatte er den Worten des Vorbesitzers vertraut, ohne sich zu vergewissern, ob die vollmundigen Beschreibungen zutreffen würden. Auf der opt. Bank war deshalb sehr schnell die Ursache in einer heftigen Dezentrierung gefunden - weil, und so ist es immer, wenn "kompetente" Finger sich über eine solche Optik "hermachen" - diese unbedarften Zeitgenossen ohne jegliche Kontrolle so ein hochwertiges Objektiv in Grund und Boden "reparieren". |
 |
C016 Fehlersuche bei einem Newton-SystemZit:"... ich habe nämlich den Eindruck, die Schärfe bricht bei Vergrößerungen ab 200-fach ein. Das sollte bei einem 10 Zoll Spiegel eigentlich nicht sein." Wo deshalb die Ursache für die "schlechte Abbildung zu suchen ist, muß man deshalb systematisch zu ermitteln suchen. Für gewöhnlich wird der Haupt-Spiegel als der "Übeltäter" gebrandmarkt, es könnte jedoch genauso gut die Lagerung von Haupt- und Fangspiegel sein, es könnte aber auch die Qualität des Fangspiegels sein. |
D090 Veloce RH 200Dr. Massimo Riccardi ist in Europa einer unserer besten Optik-Designer. Dies hat er bereits oft unter Beweis gestellt. Siehe deshalb auch mein Bericht: 2005 Clear Sky unter italienischem Himmel in Ferrara Besuch bei Massimo Ricardi. |
|
A064 Zurück zur alten SchönheitWer ein solches Objektiv öffnet, sollte sich darüber im Klaren sein, daß hinterher nichts mehr so ist, wie vorher. Jedenfalls landete dieser TMB-LZOS-APO aus dem nördlichen Teil von Europa "klappernd" bei mir: |
|
 |
~.de/Kap 06 micromamelonnage - vergeblicher Versuch einer Deutsch-Französischen DiskussionDie Frage der Oberflächenglätte eines Spiegels wird zumindestens von den französischen Sternfreunden für weitaus wichtiger gehalten, als es unsere deutschen Vertreter tun, wenn sie nicht gerade beruflich bereits vor 20 Jahren damit zu tun hatten, |
 |
H011 unser Beitrag für afa Paris - Alluna OpticsMorgen Montag geht dieses RC-System von der Firma Alluna Optics auf Reisen. Eine Abordnung der französischen Sternfreunde trifft sich morgen bei Alluna Optics, und schultert dieses nicht ganz leichte "Teil", damit es rechtzeitig in die französische Metropole gelangt. Grund genug, sich dieses "Geschoss" bei einem Sternfreund einmal aus der Nähe zu betrachten. |
C048 Drei hochwertige Dobsons ...- 12.5 Zoll ICS Spiegel |
|
D021 Erst testen - dann kaufen". . . mit der Bitte um Neujustage. ... Die Jupiter-Monde zeigen sich als schwieriger Ring, da muß etwas verstellt sein" |
|
E072 Flat 10 inch prüfenEin Kollimations-Planspiegel sollte unbedingt zwei Kriterien erfüllen: a) Die Regelmäßigkeit sollte unter PV L/10 liegen und besser. Er sollte also weder Zonen, Rillen und dergleichen haben und er sollte b) eine möglichst glatte Oberfläche haben, damit Rauhheits-Messungen mit dem Lyot-Test möglich sind. |
|
B068 Zeiss AS - ein Halb-APO f/13Die kleineren Zeiss AS-Objektive hatten schon damals die Farbreinheit heutiger Halb-APO's, auch weil sie ein Öffnungsverhältnis von etwa f/13 haben. Das bedingt eine größere Schärfentiefe, in der bestimmte optische Fehler "verschwinden". So 30 Jahre dürfte diese "Linse" schon auf dem "Buckel" haben - für den Sternfreund immer noch so wertvoll, daß er dessen opt. Eigenschaften erfahren wollte. |
|
C005 Der 24-Inch Dobson für NamibiaDie "Internationale Amateur-Sternwarte e.V." ist ein gemeinnütziger Verein, der seinen Mitgliedern die Möglichkeit bietet, an größeren Teleskopen unter einem optimalen Himmel zu beobachten und zu foto- grafieren. Optimale Beobachtungsbedingungen und gleichzeitig die Faszination des südlichen Sternenhimmels bietet Namibia, und hier insbesondere der Gamsberg. Lesen Sie hier weiter |
|
H014 Leben wie Gott in FrankenDie Gegend um Volkach ist für equisite Weine bekannt: Auslese, Beerenauslese, Trockenbeerenauslese. Optima, Scheurebe, Ortega, Rieslaner, Ruländer etc. um nur einige der fränkischen Reben zu nennen. In dieser Gegend gedeiht also auch die Hobby-Astronomie außerordentlich gut, und was die Spitzen-Weine auf der einen, das sind die Spitzen-Optiken auf der anderen Seite: Es wimmelt geradezu von Takahashis und Astreya-Optiken, |
|
 |
H002 * 2013 Die Sonne bezahlt's Sternwarte Oberreith, Chiemgau Es war eine geniale Idee, die dem Sebastian Seidl im Jahre 2006 eingefallen ist, passend zum bundesweiten |
 |
Stefans astronomische BildersammlungStefans astronomische Bildersammlung aus Volkach am Main |








